Vehicle routing problem and how to approximate a solution?

What is a vehicle routing problem (VRP)? 

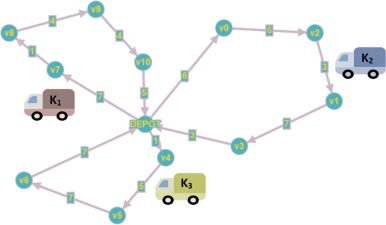
Vehicle routing problem explains the delays, inefficiencies, and cost wastage associated with transportation and fleet management. It’s a combinatorial optimization and integer programming problem that requires finding the optimal and fuel-saving route combination to carry out their operations.

The components of VRP are:

Fleet: Different types of vehicles, their specialities and capacities, fuel costs, etc.

Customer demands: The location of end users, their requirements, required quantities, delivery expectations, other orders placed by them, etc.

Routes: Routes that the delivery personnel must take covering deliveries as a one-way trip or returning to the start point.

Other considerations: Weather changes, driver working hours or route availability, special storage requirements like refrigeration, etc.

Source

No. of nodes (N) = 10

Factorial: 10! = 3628800

No. of paths = N!/2 = 1814400

Other real-world variants of VRP

VRP fundamentally belongs to logistics and transportation. But, the classic problem is applicable to many other real-world cases. Some of them include,

Shuttle services: Be it public transport or private cab services, VRP could be modeled to solve route problems that exist in picking up multiple passengers from different locations. 

Traveling salesman problem (TSP): A salesman who must meet different companies within a city, considering weather, traffic, delegate availability, personal time for lunch & break, and more constraints. Another classic that requires an algorithmic approach to finding the best route for them to cover all visits and finish on time without exhausting themselves. 

Library book reshelving: One of librarians’ day-to-day tasks involve arranging and rearranging books into the shelves, collecting them from reading desks. One can solve this complex book reshelving problem by generalizing it into a VRP.

Circuit designing: Designing physical circuits involve wiring and electrical and electrical components placement. This can be a variant of VRP, as it involves deciding the ideal length of the wire and placement of PCB boards and batteries etc, for efficient outcome without cable wastage.

Task scheduling: It can be a helpdesk center or a construction site. Scheduling employees effectively in a way that the task gets completed without labor fatigue or high labor costs requires VRP methods to solve.

Food/grocery delivery: Many food delivery services like Uber have eco-delivery as an option where multiple orders get picked up and delivered by the same person. It is an NP-hard problem given the higher number of probability for the food pickup and drop.

And, there are countless real-world problems that you can reduce to VRP while attempting to solve them. Some examples are as follows.

• Tour itinerary planning

• Marketing exhibits movement and transportation across a city

• Roosters for healthcare workers

• Load routing of electrical transmission cable 

• Security patrolling activities

• Any task scheduling problem that may or may not involve a vehicle

To sum up, all the above problems emphasize that vehicle routing problems do not always involve homogeneous/heterogeneous vehicles covering different spots over a time. And it’s a common problem across industries where VRP solutions could be applied. 

Why is the vehicle routing problem difficult to solve?

There are multiple reasons. Some due to the complexity of the problem. Some are industry-related challenges. Dynamic nature of factors could also be one of the reasons. Explaining them in detail below:

N number of possibilities to reach the destination: You can call this combinatorial explosion. Let’s say that you have 1 vehicle and 10 customers to cover. The possible routes are 10!, which equals 3,628,800. The routes will increase combinatorially if you increase the number of vehicles or customers, inviting computational complexities. This is why finding optimal routes is complex for VRP problems.  

Trying to achieve multiple objectives, not one: In most instances, you aim to achieve multiple objectives—optimized routes, high operational efficiency and labor productivity, low fuel consumption, and the like. Establishing a balance while tuning your output can be cumbersome and time-consuming.

Other constraints to consider: Every vehicle routing problem comes with a set of constraints to be wary of. 

Examples of constraints

• Delivery time window

• Driver availability and working hours

• Restraints concerning the travel path

• Unpredictable traffic and road conditions

• Two or multiple products that couldn’t be transported together

And more like this. 

Data availability: Math and AI solutions for VRP problems require data. Getting access to historical or real-time data can be a challenge for some. For example, obtaining the most reliable and accurate data on road conditions.

Industry-related challenges: In the case of logistics and transportation, changing customer preferences and demand can impact vehicle routing too. If you take eCommerce or retail, same day or next-day deliveries and on-time delivery are a few concerns affecting routing. Predicting the demand for every operating region becomes a prerequisite for a fleet unit to allot vehicles accordingly and plan the routes.

Like fluctuating demands, every domain has its own restrictions and regulations, making the combinatorial problems unsolvable or difficult to solve.

Types of vehicle routing problems

Other than VRP, following are the different route problems you might encounter.

VRPTW

VRPTW is Vehicle Routing Problem - Time Window. Here, the vehicle must deliver the product to each customer within a specific time window. Or, there will be specific servicing time allotted for each customer. 

You could imagine your Amazon delivery, for example, and the expected delivery time you see. This is an extension of classic VRP problems, but more sophisticated as another dimension of time is introduced. 

Here, the main objective is that the goods must get picked up or delivered on time while the fleet takes a near-optimal route, spending low fuel costs. While delivery and servicing time of customers plays an important role, there could be other constraints too, like the capacity of vehicles.

The complexity of VRPTW makes it a NP-Hard, and it takes heuristic or meta-heuristic methods to solve them.

CVRP

CVRP is the Capacitated Vehicle Routing Problem. Here, vehicle capacity is an important factor to consider while deciding the route to be taken. The capacity of vehicles may be limited and they are out to serve customers with known demands. For example, the weight of a fleet cannot exceed a certain kg during the starting point or at any point of its journey. Or, the volume of the item it picks up or delivers cannot exceed a known limit.

To solve the CVRP, it is necessary to find a route where the total capacity of the items being delivered does not exceed the predetermined capacity of the vehicle.

A good example of CVRP could be vehicles delivering groceries within a city with vehicles, each with a capacity of 1 ton, 3 tons, and 5ton, accordingly. The grocery shop would ensure that the vehicles cover the least amount of distance without overloading the vehicle’s capacity.

VRPPD 

VROPD is a Vehicle Routing Problem with Pickup and Delivery. This type of problem exists when the fleet driver handles both pickup and delivery consequently. Every customer servicing involves two or multiple locations, one where the order gets picked up and the rest where it’s delivered with a defined starting point. Other decision variables could be the time window for delivery (example: must be delivered 10mins within pickup) and the capacity of the vehicle. A simple example is your pizza delivery and drivers handle multiple deliveries, delivering them within 30 minutes for each customer. 

TSP

Traveling Salesman Problem is a foundational problem about a salesman who must cover multiple cities and return to the starting point, covering the shortest distance possible. 

The difference between TSP and VRP is that TSP involves one fleet (Salesman) traveling to multiple locations, where VRP involves multiple vehicles. This is why VRP is a generalization of TSP as the core problem is related. Unlike VRP, TSP doesn’t involve load limits. However, TSP could also have complex variants like mTSP involving multiple salespersons and time windows.

Ways to solve the vehicle route problem

One could relate many real-world problems to vehicle route problems. Some techniques to solve VRP and its variants, despite their complexities.

Route optimization software

A few years or decades down the road, dispatchers and fleet managers used pen and paper to create route plans for drivers. Ironically enough, this still exists in many logistics and transportation units, despite the presence of many accurate route optimization applications. 

Route optimization software works by navigating drivers through the most cost-effective routes while considering factors like real-time traffic, total no. of stops, maintenance and break, and other legal things. 

Route optimization tools available in the market: Route4Me, Scribble Maps, Salesforce Maps, OptimoRoute, and Zeo Route Planner. These tools are very helpful for logistics fleet management, field services planning, and other delivery services.

These tools collect data from multiple sources like GPS systems, traffic updates, etc., and integrate with existing customer records. Using algorithms like Dijkstra, Clarke-Wright Savings Algorithm, and nearest neighbors to analyze travel sequences, distance covered, and mileage saved. It shares the best optimized routes as visualizations for quick interpretation.

Google OR tools

Developed by Google, OR tools is an open source software to solve large-scale vehicle routing problems, integer programming, constraint programming, etc. 

OR tools are suitable for all variants of VRP, including capacity constraints, simultaneous pickups and deliveries, time window constraints, etc. It can also solve knapsack problems, ensuring the maximum number of items being packed without exceeding the overall capacity.

Being a highly versatile and scalable tool, it’s great for solving real-world problems like vehicle routing, shift planning, resource allocation, etc.

If you want to use OR tools to find near-optimal routes, you can access it through languages like Python, C++, Java, and C#. 

A seasoned data scientist is all you need to modify and train the model to suit your specific requirements.

Approximation algorithms

VRP and its variants are NP-hard problems. Meaning, it can be impossible to extract the best and optimal solution in polynomial time. That’s where approximation algorithms can help. The goal is to get a near-optimal solution within the runtime. 

For example, among a collection of costs required to perform a certain job, an approximation algorithm can find a near-minimum or near-maximum cost, depending on the objective. 

Some real-time examples that you can solve with approximation algorithms are vehicle routing, minimum vector cover problem, and other optimization problems. 

We know that the approximate algorithm solution ≠ optimal solution. To validate how close the former is to the latter, we can use approximation ratios. If the approximation ratio value is equal to 1, then the obtained is the optimal solution. This is why ML engineers often try bringing this performance ratio value closer to 1 to get the best feasible solution.

Heuristics and meta-heuristics approach

We already saw how route optimization software uses algorithms based on heuristics and meta-heuristics. If you are building a custom solution for VRP and other NP-Hard problems, then these algorithms can be one of the practical choices. 

Heuristics: Their solutions are often based on a rule of thumb. It tries offering the most practical solution in the shortest possible time. Some algorithms are greedy algorithms, Clarke and Wright savings algorithms, nearest neighbors (especially for the traveling salesman problem), etc.

Meta-heuristics: While heuristic algorithms fit only specific problems, meta-heuristics can fit any problem and offer high-quality solutions. They are known for establishing balance through exploration and exploitation, making use of existing solutions, while looking for new ones. Some examples are ant colony optimization, genetic algorithms, etc. 

Custom designed data structures

By changing the way a company manages, processes, and manipulates the data, you could make them more suitable and fit to solving complex problems like vehicle routing. Like designing a custom wrench for a specific type of bolt, having a custom data design helps speed up the process with more promising outcomes. 

Custom data structures can come in handy for optimization algorithms as they have many use cases and requirements—reducing computational complexity, dealing with constraints, parallel processing, etc.

Example: Setting up queues with priority values that speeds up shortest path and search algorithms.​ Other most utilized data structures include K-dimensional tree, disjoint set union, etc.

Why should you resolve vehicle routing problems?

Solving vehicle routing problems is hard. But it has so many advantages. 

Better customer service

‘Where is my order?’ is one of the most asked questions every customer service unit faces; it can be a food delivery or a grocery chain or an eCommerce business. Optimizing vehicle routing is one way to fix it. There can still be many unexpected scenarios, but a near-optimal solution is a promising and more efficient way to reduce the travel hours by the agent. 

Reduce unwanted costs

One of the top 5 costs for shipping, logistics, and distribution is fuel and labor costs. A company can curb both by going for a route optimization solution. These are not only expensive but can be unforeseen too. Credits: fluctuating fuel costs, unexpected route closing or changes, OT by drivers, and more. Solving the VRP problem is how you can place a tab on these spiking expenses. 

Time management

Present day businesses strive to be agile and responsive to market changes. However, they face many struggles and unexpected delays, especially with the last-mile delivery. Vehicle routing solutions can help you reduce the time wasted while bringing certainty to your business.

Resource management

Whether it’s vehicle routing or waste collection, it all boils down to navigating people through a cost-efficient and fast route. By using vehicle routing solutions, companies and teams can effectively manage their resources, ensuring optimal utilization without causing excessive strain.

Final thoughts

With the amount of advancements in math, ML, and AI areas, optimization problems are no longer unsolvable. Even though a best route couldn’t be guaranteed, we could track down and find a decent solution for large instances. 

While there are out-of-the-box solutions available for VRP problems, it cannot be generalized to solve all VRP variants we saw in the above sections. That’s where you need a team of data scientists equipped with domain knowledge to solve the problem and technical expertise to choose the right or custom solution.  

We recently solved one such problem for a logistics tech partner, which helped them generate near-optimal placement suggestions for rectangular warehouse units. This saved them 13 to 15% of the labor movement for those engaged in the picking process. 

Read the full story of how we identified a near-optimal SKU arrangement solution, solving the logistics picking problem.